需要指导、转载等,请联系作者 Lewis XU(Email: xuwei3893@gmail.com)。
引言
列生成算法是一种解决大规模整数规划的框架,比直接使用商业求解器求解模型的速度要快。再次框架下,将问题分解为主问题(Restricted Master Problem,RMP)和子问题(SubProblem,SP)。子问题是求解一种可行的子方案,主问题则用来求解原问题的目标,而子问题的目标则是主问题的检验数。一个子问题的解,能够添加进主问题,对最小化问题而言,子问题的目标函数必须为负。列生成就是不断的求解子问题,把子问题逐个的添加进主问题中,直到子问题的解不满足条件。
Cutting Stock Problem 问题描述
给定了若个根长度为$L$钢管,有$n$种钢管长度的订单,即长度为$l_i$的需求为$b_i$,求最少需要多少根这样的钢管才能满足需求?
在本文中,假定每根钢管长度$L=17m$,需要3米、6米、9米的钢管各25、20、18根,即$l = [3m,6m,9m]$,$b=[25,20,18]$。
整数规划模型
设给定$N$根长度为$L$的钢管,有$I$种钢管的需求,长度为$l_i$的需求量为$b_i$根。记$y_n$为0-1变量,如果第$n$根钢管被使用为1,否则为0。记$x_i^n$为第$n$根钢管被切了长度为$l_i$的长度的数量。由此,建立以下数学模型(\ref{eq:obj})-(\ref{eq:y}):
\begin{equation} \min\sum_{n\in N}y_n \label{eq:obj}\tag{1} \end{equation} subject to: \begin{equation} \sum_{n\in N}x_i^n\geqslant b_i, \forall i \in I \label{eq:demand}\tag{2} \end{equation} \begin{equation} \sum_{i=1}^{I}l_i x_i^n\leqslant Ly_n, \forall n\in N \label{eq:length}\tag{3} \end{equation} \begin{equation} x_i^n\in \mathcal{Z}^+, \forall i \in I, \forall n\in N \label{eq:x}\tag{4} \end{equation} \begin{equation} y_n\in{0,1}, \forall n\in N \label{eq:y}\tag{5} \end{equation}
公式(\ref{eq:obj})表示最小化钢管数量,公式(\ref{eq:demand})表示每种钢管的数量得到满足,公式(\ref{eq:length})表示每根钢管的切割的长度总和不超过$L$.(\ref{eq:x})-(\ref{eq:y})则定义了变量$x_i^n$和$y_n$的定义域。
Column Generation
该问题可以等价于以下描述:一根钢管有不同的切割方案,比如17$m$可以切成5根3$m$的,也可以切成1根3$m$、2根6$m$的…。我们的目标是从这些方案中,选出消耗钢材数量最小的组合,以满足各个长度的数量。
我们首先确定主问题的模型。设当前一共有P种切割方案,第$p$种方案钢管切长度为$l_i$的切割数量为$a_{ip}$,第$p$种方案出现了$z_p$次。由此,主问题模型为公式(\ref{eq:mpobj})-(\ref{eq:mpz}): \begin{equation} \min \sum_{p\in P}z_p \label{eq:mpobj}\tag{6} \end{equation} subject to: \begin{equation} \sum_{p\in P}a_{ip}z_p\geqslant b_i, \forall i\in I \label{eq:mpdemand}\tag{7} \end{equation} \begin{equation} z_p\in \mathcal{Z}^+,\forall p\in P \label{eq:mpz}\tag{8} \end{equation}
公式(\ref{eq:mpobj})是使钢管数量最小,公式(\ref{eq:mpdemand})则是满足所有的需求。
主问题
一次性找出所有的满足条件的模式是不现实的,我们先给定一些初始可行解$P’$,能够满足所有的需求,在通过子问题,不断求出新的可行方案,添加到$P’$中,直到达到最优解即可。 \begin{equation} \min \sum_{p\in P’}z_p \label{eq:rmpobj}\tag{9} \end{equation} subject to: \begin{equation} \sum_{p\in P’}a_{ip}z_p\geqslant b_i, \forall i\in I \label{eq:rmpdemand}\tag{10} \end{equation} \begin{equation} z_p\geqslant 0,\forall p\in P’ \label{eq:rmpz}\tag{11} \end{equation}
如何寻找初始解?
显然,这种切割方式过于粗糙。下面,通过子问题来生成更多的可行方案,将这些粗糙的方案踢出去(实际上就是单纯形法的出基)。
子问题
子问题是求一种可行的切割方案,使得把这种方案添加进去之后(实际上就是单纯形法的入基),主问题的目标函数能下降最多,所以正如引言所说,子问题的目标函数是使主问题的校验数最小。设$\pi_i$是主问题中第$i$个约束的对偶值,所以,子问题的模型如下:
\begin{equation} \min 1-\sum_{i\in I}a_{ip}\pi_i \label{eq:spobj}\tag{12} \end{equation} subject to: \begin{equation} \sum_{i\in I}l_i a_{ip} \leqslant L \label{eq:splength}\tag{13} \end{equation} \begin{equation} a_{ip}\in\mathcal{Z}^+, \forall i\in I \label{eq:spa}\tag{14} \end{equation}
公式(\ref{eq:splength})就是限制切割方案的长度,目标函数(\ref{eq:spobj})则是主问题的检验数。
不断的进行迭代,直到子问题的解大于等于0(对于最小化问题),就可以结束了。
算例
寻找初始解
只要将每根钢管按照同一种长度来切,一定能切出满足条件的组合。
所以初始解的方式:
- 全切成3m以满足3m的需求,一根可以切出$\lfloor\frac{17}{3}\rfloor$= 5根;
- 全切成6m以满足6m的需求,一根可以切出$\lfloor\frac{17}{6}\rfloor$= 2根;
- 全切成9m以满足9m的需求,一根可以切出$\lfloor\frac{17}{9}\rfloor$= 1根。
也就是说,初始主问题模型: \begin{equation} \min z_1 + z_2 + z_3 \end{equation} \begin{equation} 5z_1 + 0z_2 + 0z_3 \geqslant 25 \end{equation} \begin{equation} 0z_1 + 2z_2 + 0z_3 \geqslant 20 \end{equation} \begin{equation} 0z_1 + 0z_2 + 1z_3 \geqslant 18 \end{equation} \begin{equation} z_1, z_2, z_3 \geqslant 0 \end{equation}
第一次迭代
解得各个约束的对偶值$\pi = [\pi_1, \pi_2, \pi_3] = [0.2,0.5,1]$. 所以,子问题为: \begin{equation} \min 1-0.2a_{1,new}-0.5a_{2,new}-a_{3,new} \end{equation} \begin{equation} 3a_{1,new}+6a_{2,new}+9a_{3,new}\leqslant 17 \end{equation} \begin{equation} a_{1,new},a_{2,new},a_{3,new} \in \mathcal{Z}^+ \end{equation} 解得$a_{i,new} = [a_{1,new},a_{2,new},a_{3,new}] = [0,1,1]$,并且子问题的目标函数为-0.5<0,需要继续迭代。
所以,添加新变量$z_4$到主问题模型: \begin{equation} \min z_1 + z_2 + z_3 + z_4 \end{equation} \begin{equation} 5z_1 + 0z_2 + 0z_3 + 0z_4 \geqslant 25 \end{equation} \begin{equation} 0z_1 + 2z_2 + 0z_3 + z_4\geqslant 20 \end{equation} \begin{equation} 0z_1 + 0z_2 + 1z_3 + z_4 \geqslant 18 \end{equation} \begin{equation} z_1, z_2, z_3,z_4 \geqslant 0 \end{equation}
第二次迭代
继续求解主模型,得到各个约束的对偶值$\pi = [\pi_1, \pi_2, \pi_3] = [0.2,0.5,0.5]$. 所以,子问题为: \begin{equation} \min 1-0.2a_{1,new}-0.5a_{2,new}-0.5a_{3,new} \end{equation} \begin{equation} 3a_{1,new}+6a_{2,new}+9a_{3,new}\leqslant 17 \end{equation} \begin{equation} a_{1,new},a_{2,new},a_{3,new} \in \mathcal{Z}^+ \end{equation} 解得$a_{i,new} = [a_{1,new},a_{2,new},a_{3,new}] = [1,2,0]$,并且子问题的目标函数为-0.2<0,需要继续迭代。
所以,添加新变量$z_5$到主问题模型: \begin{equation} \min z_1 + z_2 + z_3 + z_4 + z_5 \end{equation} \begin{equation} 5z_1 + 0z_2 + 0z_3 + 0z_4 + z_5 \geqslant 25 \end{equation} \begin{equation} 0z_1 + 2z_2 + 0z_3 + z_4 + 2z_5\geqslant 20 \end{equation} \begin{equation} 0z_1 + 0z_2 + 1z_3 + z_4 + 0z_5\geqslant 18 \end{equation} \begin{equation} z_1, z_2, z_3,z_4,z_5 \geqslant 0 \end{equation}
第三次迭代
继续求解主模型,得到各个约束的对偶值$\pi = [\pi_1, \pi_2, \pi_3] = [0.2,0.4,0.6]$. 所以,子问题为: \begin{equation} \min 1-0.2a_{1,new}-0.4a_{2,new}-0.6a_{3,new} \end{equation} \begin{equation} 3a_{1,new}+6a_{2,new}+9a_{3,new}\leqslant 17 \end{equation} \begin{equation} a_{1,new},a_{2,new},a_{3,new} \in \mathcal{Z}^+ \end{equation} 解得$a_{i,new} = [a_{1,new},a_{2,new},a_{3,new}] = [1,2,0]$,并且子问题的目标函数为0,不需要继续迭代。
最终结果
\begin{equation} \min z_1 + z_2 + z_3 + z_4 + z_5 \end{equation} \begin{equation} 5z_1 + 0z_2 + 0z_3 + 0z_4 + z_5 \geqslant 25 \end{equation} \begin{equation} 0z_1 + 2z_2 + 0z_3 + z_4 + 2z_5\geqslant 20 \end{equation} \begin{equation} 0z_1 + 0z_2 + 1z_3 + z_4 + 0z_5\geqslant 18 \end{equation} \begin{equation} z_1, z_2, z_3,z_4,z_5 \geqslant 0 \end{equation}
所以第二次得到的主模型为最终模型,求解得到$\sum_{i=1}^{5} z_i = 24$。
运行截图
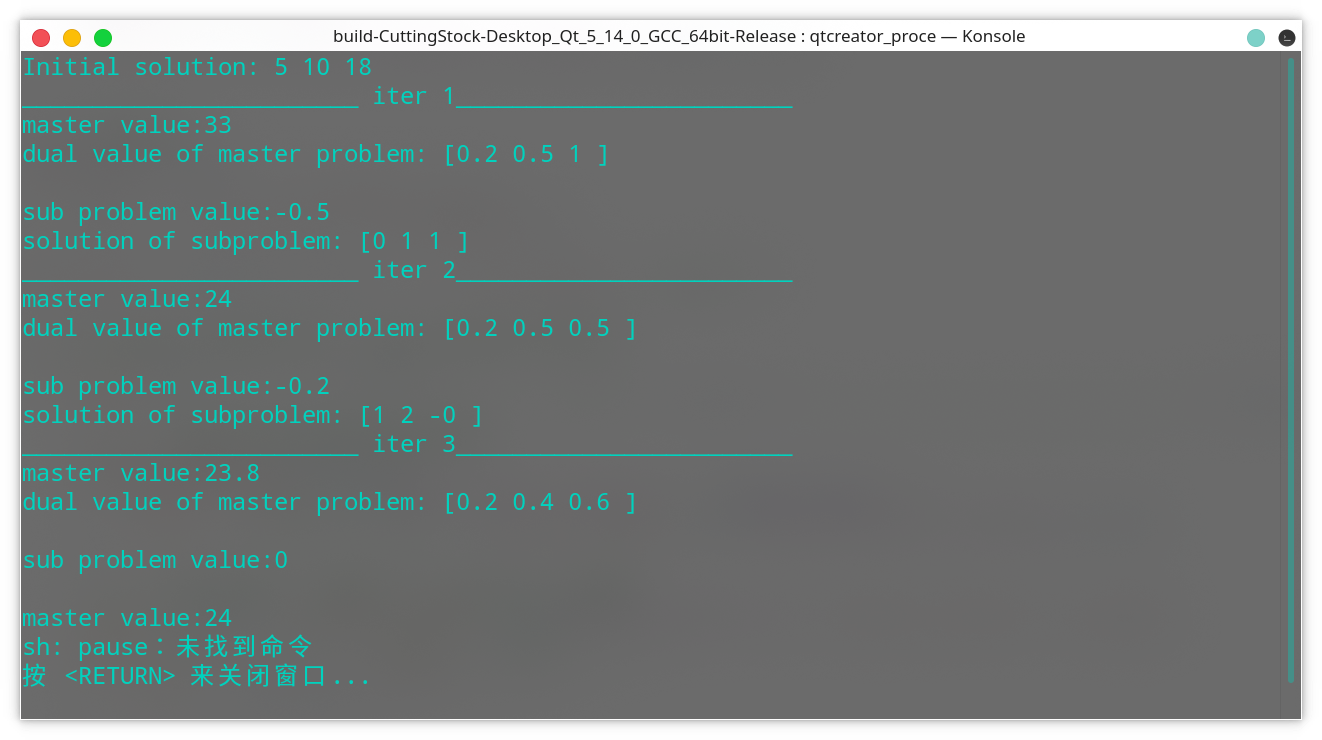
规律总结
- 主问题:只添加新变量以及各个约束新变量对应的系数。
- 子问题:只改变目标函数的系数,将满足检验数条件的解作为新变量的系数添加到主问题,不断迭代。
C++代码
使用GUROBI求解器进行求解,请先安装。
/*
描述:用列生成求解CuttingStock:C++11 Gurobi 8.1.1
Author: Lewis XU
日期:2020-05-19
见解:Gurobi对指针很友好,大部分的API都使用指针作为参数,这也是性能比CPLEX好的地方。
本案例中,若是使用指针,代码量会减少特别多。可以少使用很多循环语句。
*/
#include <iostream>
#include <vector>
#include <sstream>
#include <gurobi_c++.h>
using namespace std;
class CutStock {
public:
CutStock() = delete;
CutStock(const CutStock&) = delete;
~CutStock() {
//手动释放资源
delete sub_model;
delete master_model;
delete env;
}
//带参数构造
CutStock(const int rollLength, const vector<double>& nDemands, const vector<double>& nAmounts)
:m_rollLength(rollLength), m_nDemands(nDemands), m_nAmounts(nAmounts) {
m_type = nDemands.size();
env = new GRBEnv();//new->delete
}
//建模型
void solve() {
try {
//1.建立松弛主问题
//1.1主问题模型
master_model = new GRBModel(*env);
master_model->set(GRB_IntParam_OutputFlag, false);
master_model->set(GRB_StringAttr_ModelName, "mastar_slack_model");
master_model->set(GRB_IntAttr_ModelSense, GRB_MINIMIZE);
//1.2添加m_type个约束
master_constrs = master_model->addConstrs(m_type);
//1.3确定每个约束的右侧值
for (int i = 0; i < m_type; ++i) {
master_constrs[i].set(GRB_CharAttr_Sense, GRB_GREATER_EQUAL);
master_constrs[i].set(GRB_DoubleAttr_RHS, m_nAmounts[i]);
ostringstream cname;
cname << "type" << i;
master_constrs[i].set(GRB_StringAttr_ConstrName, cname.str());
}
//1.4按列添加变量
cout<<"Initial solution: ";
for (int i = 0; i < m_type; ++i) {
cout<<int(m_nAmounts[i]/int(m_rollLength / m_nDemands[i]))<<" ";
GRBColumn column = GRBColumn();
column.addTerm(int(m_rollLength / m_nDemands[i]), master_constrs[i]);
ostringstream vname;
vname << "x" << i;
master_model->addVar(0, GRB_INFINITY, 1, GRB_CONTINUOUS, column, vname.str());
}
cout<<endl;
master_model->write("master0.lp");
//2.建立最小化reduce price的目标的子问题
//2.1建立子问题模型
sub_model = new GRBModel(*env);
sub_model->set(GRB_IntParam_OutputFlag, false);
sub_model->set(GRB_StringAttr_ModelName, "sub_model");
sub_model->set(GRB_IntAttr_ModelSense, GRB_MINIMIZE);
//2.2添加变量
sub_var = sub_model->addVars(m_type, GRB_INTEGER);
for (int i = 0; i < m_type; ++i) {
sub_var[i].set(GRB_DoubleAttr_LB, 0);
sub_var[i].set(GRB_DoubleAttr_UB, m_rollLength);//这里可以设置为GRB_INFINITY
ostringstream vname;
vname << "x" << i;
sub_var[i].set(GRB_StringAttr_VarName, vname.str());
}
//2.3添加约束
GRBLinExpr expr;
for (int i = 0; i < m_type; ++i) {
expr += sub_var[i] * m_nDemands[i];
}
sub_model->addConstr(expr <= m_rollLength, "length");
//3.迭代求解子问题和添加列、求解主问题直至没有新列
for (int iter = 1; ; ++iter) {
cout << "________________________ iter "<< iter << "________________________" << endl;
//3.1 求解主问题,得到约束的对偶值
master_model->optimize();
if (master_model->get(GRB_IntAttr_Status) == GRB_OPTIMAL) {
cout << "master value:"<<master_model->get(GRB_DoubleAttr_ObjVal)<<endl;
}
//3.2 获得对偶值。使用指针,所以很方便,不用循环
double *price = master_model->get(GRB_DoubleAttr_Pi, master_constrs, m_type);
cout<<"dual value of master problem: [";
for (int i = 0; i < m_type; ++i) {
cout << price[i] << " ";
}
cout<<"]"<<endl;
//3.3 设置子问题的目标函数
GRBLinExpr expr(-1);
expr.addTerms(price, sub_var, m_type);
sub_model->setObjective(-expr, GRB_MINIMIZE);
//3.4 求解子问题
sub_model->optimize();
ostringstream sub_name;
sub_name << "sub" << iter << ".lp";
sub_model->write(sub_name.str());
if (sub_model->get(GRB_IntAttr_Status) == GRB_OPTIMAL) {
cout << "\nsub problem value:"<<
sub_model->get(GRB_DoubleAttr_ObjVal) << endl;
if (sub_model->get(GRB_DoubleAttr_ObjVal) > -0.000001) {
break;
}
}
//3.4 获取子问题的新解
double* pattern = sub_model->get(GRB_DoubleAttr_X, sub_var, m_type);
cout<<"solution of subproblem: [";
for(int i=0; i<m_type; ++i) {
cout<<pattern[i]<<" ";
}
cout<<"]"<<endl;
//3.5 添加新列
ostringstream vname;
vname << "x" << m_type + iter;
master_model->addVar(0, GRB_INFINITY, 1, GRB_CONTINUOUS, m_type, master_constrs, pattern,vname.str());
ostringstream master_name;
master_name << "model" << iter << ".lp";
master_model->write(master_name.str());
delete price;
delete pattern;
}
master_var = master_model->getVars();
int numVars = master_model->get(GRB_IntAttr_NumVars);
for (int i = 0; i < numVars; ++i) {
master_var[i].set(GRB_CharAttr_VType, GRB_INTEGER);
}
master_model->write("result.lp");
master_model->optimize();
if (master_model->get(GRB_IntAttr_Status) == GRB_OPTIMAL) {
cout << "\nmaster value:" << master_model->get(GRB_DoubleAttr_ObjVal) << endl;
}
} catch (GRBException& e) {
cerr << e.getErrorCode() << e.getMessage() << endl;
}
}
private:
//Cutting stock的变量,模型所需的参数
int m_rollLength;
//可用钢材的长度
int m_type;
vector<double> m_nDemands; //n种钢材长度需求
vector<double> m_nAmounts; //n种钢材需求数量
//GRB建模相关的变量
GRBEnv* env;//GRB环境
GRBModel *master_model,//主问题松弛模型
*sub_model;//子问题求新的可添加列列
GRBVar *master_var,//主问题的变量
*sub_var;//子问题的变量
GRBConstr *master_constrs; //主问题的约束
};
int main() {
int length = 17;
vector<double> demands = { 3, 6, 9};
vector<double> amounts = { 25, 20, 18 };
CutStock model(length, demands, amounts);
model.solve();
system("pause");
return 0;
}
需要指导、转载等,请联系作者 Lewis XU(Email: xuwei3893@gmail.com)。